Las funciones trigonométricas surgen de una forma natural al estudiar el triángulo rectángulo y observar que las razones (cocientes) entre las longitudes de dos cualesquiera de sus lados sólo dependen del valor de los ángulos del triángulo. Pero vayamos por partes.
Primero consideraremos triángulos rectángulos ABC, rectángulos en A, con <B = 60º y <C = 30º. Todos los triángulos que dibujemos con estos ángulos son semejantes, y, por ello, las medidas de sus lados proporcionales:

*SISTEMA SEXAGESIMAL Y CIRCULAR:
El sistema sexagesimal es un sistema de numeración en el que cada unidad se divide en 60 unidades de orden inferior, es decir, es su sistema de numeración en base 60. Se aplica en la actualidad a la medida del tiempo y a la de la amplitud de los ángulos. 1 h 60 min 60 s 1º 60' 60'' Operaciones en el sistema sexagesimal Suma 1er paso Se colocan las horas debajo de las horas (o los grados debajo de los grados), los minutos debajo de los minutos y los segundos debajo de los segundos; y se suman. 2o paso Si los segundos suman más de 60, se divide dicho número entre 60; el resto serán los segundos y el cociente se añadirá a los minutos. 3er paso Se hace lo mismo para los minutos. Resta 1er paso Se colocan las horas debajo de las horas (o los grados debajo de los grados), los minutos debajo de los minutos y los segundos debajo de los segundos. 2o paso Se restan los segundos. Caso de que no sea posible, convertimos un minuto del minuendo en 60 segundos y se lo sumamos a los segundos del minuendo.
A continuación restamos los segundos. 3er paso Hacemos lo mismo con los minutos. Multiplicación por un número 1er paso Multiplicamos los segundos, minutos y horas (o grados) por el número. 2o paso Si los segundos sobrepasan los 60, se divide dicho número entre 60; el resto serán los segundos y el cociente se añadirán a los minutos. 3er paso · Se hace lo mismo para los minutos. División por un número Dividir 37º 48' 25'' entre 5 1er paso Se dividen las horas (o grados) entre el número. 2o paso El cociente son los grados y el resto, multiplicando por 60, los minutos. 3er paso · Se añaden estos minutos a los que tenemos y se repite el mismo proceso con los minutos. 4o paso Se añaden estos segundos a los que tenemos y se dividen los segundos. Medida compleja Es aquella que expresa distintas clases de unidades: 3 h 5 min 7s 25° 32' 17''. Medida incompleja o simple Se expresa únicamente con una clase de unidades. 3.2 h 5.12º. Paso de medidas complejas a incomplejas Para pasar de medidas complejas a incomplejas hay que transformar cada una de las unidades que tenemos en la que queremos obtener, como resultado final. Pasar a segundos 3 h 36 min 42 s. Paso de medidas incomplejas a complejas Tenemos dos casos: 1 Si queremos pasar a unidades mayores hay que dividir. 7520'' 2 Si queremos pasar a unidades menores hay que multiplicar. El sistema circular. En este sistema se usa como unidad el ángulo llamado "radián". Un radián, es el ángulo cuyos lados comprenden un arco a la circunferencia cuya longitud es igual al radio de la circunferencia. Un radián equivale a 57° 17’ 44.81‘’ Para encontrar la medición de cualquier ángulo utilizamos el transportador, que usualmente está dividido en 360 partes iguales y cada una de esas partes equivalen a un grado, es decir, está en el sistema sexagesimal. Para encontrar qué tantos grados hay en ángulo, utilizando el transportador, se procede como sigue. 1.- Se hace coincidir la referencia y el cero del transportador con el vértice, de tal modo, que la parte horizontal de la referencia, ( ^ ) con el lado horizontal del ángulo y el otro lado del ángulo marcará en el transportador la magnitud del mismo.
*Razones trigonometricas directas y reciprocas de angulos agudos:
Dado un triángulo rectángulo ABC, se definen las razones trigonométricas del ángulo  , de la siguiente manera:
, de la siguiente manera:
 , de la siguiente manera:
, de la siguiente manera:
|
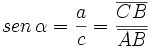
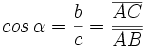
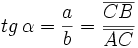
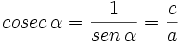
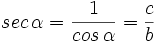
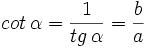

No hay comentarios.:
Publicar un comentario